At AllTheScience, we're committed to delivering accurate, trustworthy information. Our expert-authored content is rigorously fact-checked and sourced from credible authorities. Discover how we uphold the highest standards in providing you with reliable knowledge.
What is the Associative Property?
The associative property of mathematics refers to the ability to group certain numbers together in specific mathematical operations, in any type of order without changing the answer. Most commonly, children begin to study the associative property of addition and then move on to study the associative property of multiplication. With both these operations, changing the order of the numbers being added or numbers being multiplied won’t result in a changed sum or product.
Some confuse the associative property with the commutative property, but the commutative property tends to apply to two numbers only. In contrast, the associative property is often used to express the unchanging nature of sums or products when three or more numbers are used. The property may also be discussed in relationship to how parentheses are used in math. Placing parentheses around some of the numbers that will all be added together doesn’t change the results.
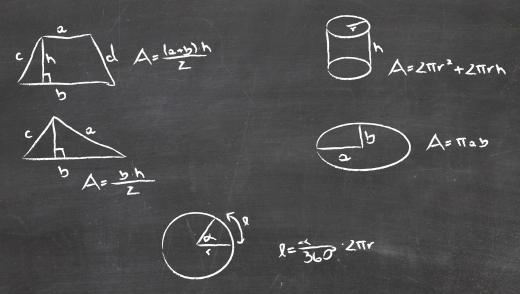
Consider the following examples:
1 + 2 + 3 +4 = 10. This will remain true even if the numbers are grouped differently.
(1 + 3) + (2 + 4) and (1 + 2 + 3) + 4 both equal ten. You don’t have to consider the order of these numbers or their grouping since the act of adding means they will still have the same total sum.
In the associative property of multiplication, the same basic idea holds true. A X B X C = (AB)C or (AC)B. No matter how you group these numbers together, product remains constant.
Especially in multiplication, the associative property can prove very helpful. Take for instance the basic formula for calculating the area of a triangle: 1/2bh or half of the base times the height. Now consider that the height is 4 inches and the base is 13 inches. It is simpler to take half of height (4/2 = 2) than it is to take half of the base (13/2 = 6.5). It’s a lot easier to solve the resultant problem 2 X 13 than it is to solve 6.5 X 4.
We can do this when we understand the associative property because we will know that it doesn’t matter what order we multiply these numbers in. This can take the work out of some complicated calculations and make math work just a little bit easier. Note that this property does not work when you use division or subtraction. Changing order and grouping with these operations will impact results.
AS FEATURED ON:
AS FEATURED ON:











Discuss this Article
Post your comments