At AllTheScience, we're committed to delivering accurate, trustworthy information. Our expert-authored content is rigorously fact-checked and sourced from credible authorities. Discover how we uphold the highest standards in providing you with reliable knowledge.
What is Standard Deviation?
Standard deviation is a statistical value used to determine how spread out the data in a sample are, and how close individual data points are to the mean — or average — value of the sample. A standard deviation of a data set equal to zero indicates that all values in the set are the same. A larger value implies that the individual data points are farther from the mean value.
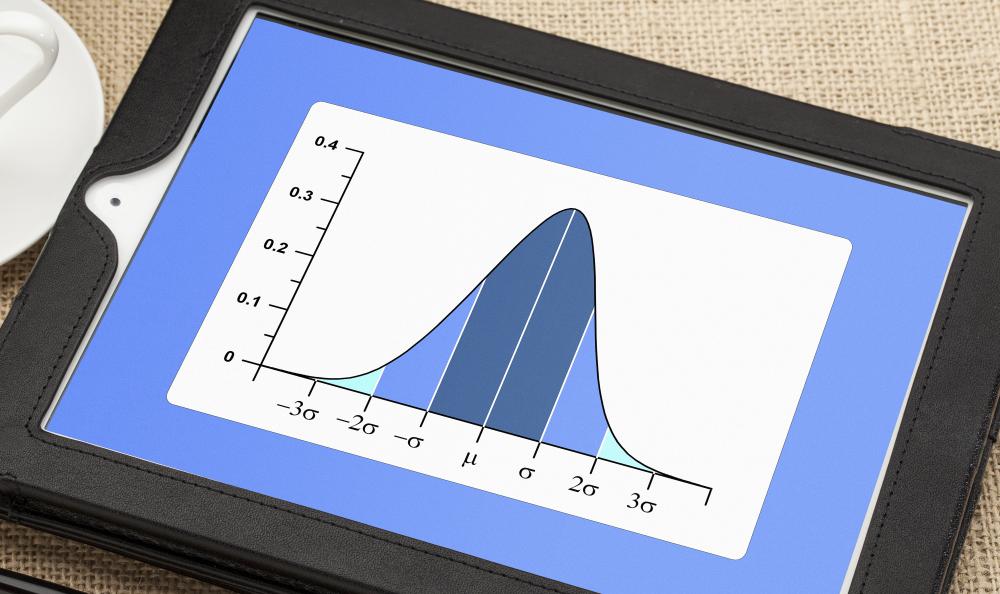
In a normal distribution of data, also known as a bell curve, the majority of the data in the distribution — approximately 68% — will fall within plus or minus one standard deviation of the mean. For example, if the standard deviation of a data set is 2, the majority of data in the set will fall within 2 more or 2 less than the mean. Roughly 95.5% of normally distributed data is within two standard deviations of the mean, and over 99% are within three.
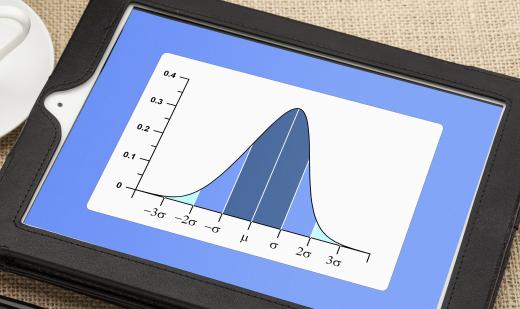
To calculate the standard deviation, statisticians first calculate the mean value of all the data points. The mean is equal to the sum of all the values in the data set divided by the total number of data points. Next, the deviation of each data point from the average is calculated by subtracting its value from the mean value. Each data point's deviation is squared, and the individual squared deviations are averaged together. The resulting value is known as the variance. Standard deviation is the square root of the variance.
Typically, statisticians find the standard deviation of a sample from a population and use that to represent the entire population. Finding the exact data for a large population is impractical, if not impossible, so using a representative sample is often the best method. For example, if someone wanted to find the number of adult men in the state of California who weighed between 180 and 200 pounds, he could measure the weights of a small number of men and calculate their average, variance and standard deviation, and assume that the same values hold true for the population as a whole.
In addition to the statistical analysis uses, standard deviation can also be used to determine the amount of risk and volatility associated with a particular investment. Investors can calculate the annual standard deviation of an investment's returns and use that number to determine how volatile the investment is. A larger standard deviation would imply a more risky investment, assuming that stability was the desired result.
AS FEATURED ON:
AS FEATURED ON:








Discussion Comments
How can you compare data between three probabilities? Say you have an amount of data points, and you are asked about three different probabilities: .25, .5, and .75. If you have calculated the mean and the standard deviation for all three, what can we deduce from the information?
Thanks, very helpful. I now have a better picture of what it means.
Thank you for the simple, straightforward explanation. Now, how do I get my teacher to explain things as well?
Thanks for this, helped lots!
Thank you for the info. I could have skipped the first two weeks of my semester, had I found this post sooner.
very helpful - explained better than my maths teacher.
clear enough to be useful.
Informative. Thank you.
Post your comments