At SmartCapitalMind, we're committed to delivering accurate, trustworthy information. Our expert-authored content is rigorously fact-checked and sourced from credible authorities. Discover how we uphold the highest standards in providing you with reliable knowledge.
What Is Skewed Distribution?
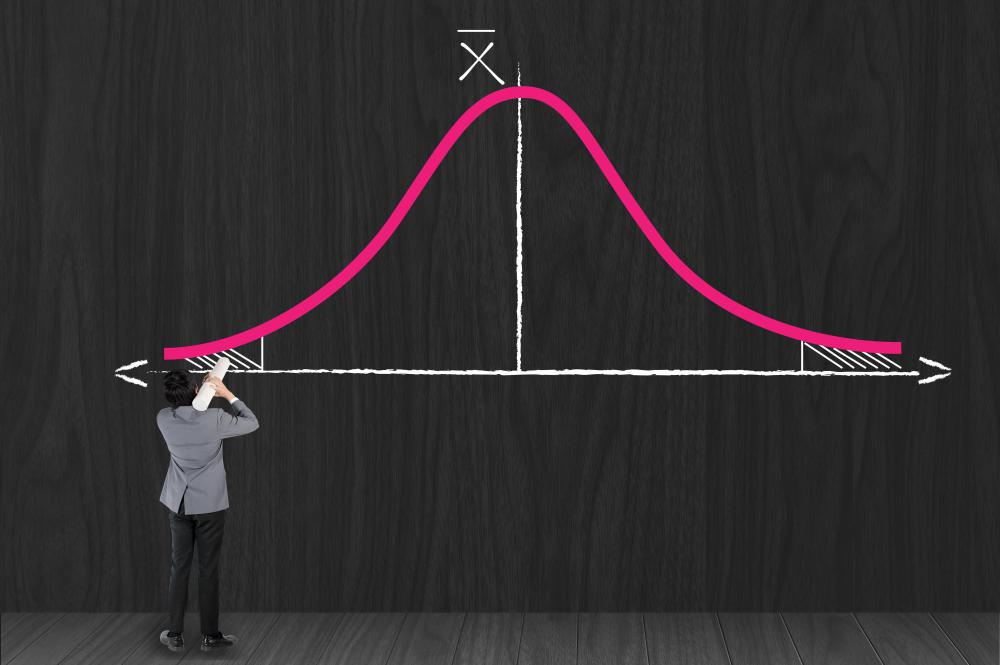
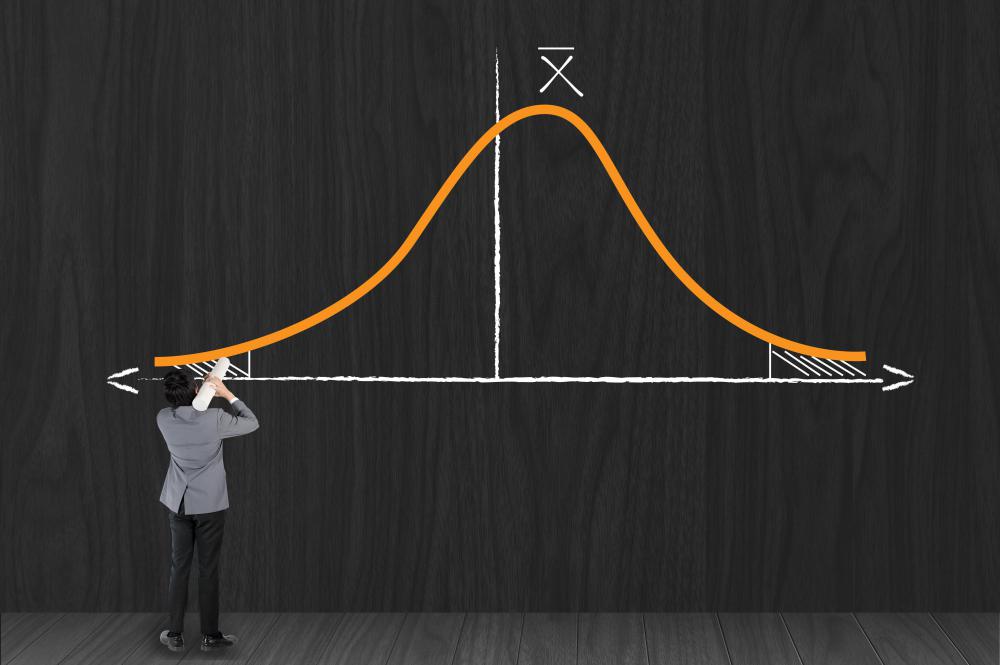
A skewed distribution refers to a probability distribution that is uneven and asymmetric in nature. Unlike a standard normal distribution, which resembles a bell curve in shape, skewed distributions are shifted to one side, possessing a longer tail on one side relative to the other side of the median. The other side of the curve will possess a clustered peak of values where the majority of data points occur. This type of distribution curve is usually classified as having either a positive skew or a negative skew, depending on the direction of the curve's shift.
Generally, a skewed distribution is said to possess positive skew if the tail of the curve is longer on the right side when compared to the left side. This skewed distribution is also referred to as skewed to the right because the right side possesses the wider extension of data points. Positive skew curves possess the largest number of values toward the left side of the curve.

In contrast, negatively skewed distributions possess the most data points on the right side of the curve. These curves have longer tails on the left sides, so they are said to be skewed to the left. An important rule in determining the direction of skew is to consider the length of the tail rather than the location of the mean or median. This is because the skew is ultimately caused by the furthest outlying values, which stretch the curve out toward that side of the graph.

Understanding the properties of a skewed distribution is important in many statistical applications. Many people assume that data follows a bell curve, or normal distribution, so they also assume that a graph has zero skewness. These assumptions, however, could lead them to misinterpret information about the actual distribution.
A skewed distribution is inherently uneven in nature, so it will not follow standard normal patterns such as standard deviation. Normal distributions involve one standard deviation that applies to both sides of the curve, but skewed distributions will have different standard deviation values for each side of the curve. This is because the two sides are not mirror images of each other, so the equations describing one side cannot be applied to the other. The standard deviation value is generally larger for the side with the longer tail because there is a wider spread of data on that side when compared to the shorter tail.
AS FEATURED ON:
AS FEATURED ON:








Discussion Comments
Kurtosis does not measure anything about the "peak" as was historically reported. Rather, it is a measure of whether there are outliers (ie, rare extreme values) in the data. These show up in graphs as one or a very few points that are very far from the main body of the data.
Can anyone help me understand skewed distribution for my presentation. I can't seem to understand about graphs.
In my stats class today, the teacher mentioned that curves can have different levels of skewness and kurtosis. She didn't go into any real detail explaining what this is, especially kurtosis.
Could someone give me a brief explanation to help point me in the right direction as to what kurtosis means?
@cardsfan27 - Great examples. I'm not sure why I couldn't think of those. When I was thinking of something like population that would have a right skewed distribution. There are many more young people than there are old people. I guess something else could be the size of trees in a forest. There are hundreds of seedlings and saplings for every tree that is fully grown.
I did some more research on the curves with two high points. They are called bimodal distributions. All of the examples I found were similar to yours and involved height or weight. I would be interested to hear more of them, though.
@titans62 - I'm having the opposite problem! All I can think of are things that have a normal distribution, but are not skewed. Some of the things I'm thinking of that would be a normal bell shape are height and weight of the population. Test scores are also a stereotypical bell curve example.
Your second question had me stumped for a few minutes, but I think I've got an example. This might be a little far fetched, but maybe someone else has a better one. If you took 25 men and 25 women, and then took their weights. You could assume that the men are going to weigh more on average than the women, so if you graphed the weights, you might find that the women make a peak lower on the scale, and men make a peak farther up. I hope that made sense.
Can someone help me -- I understand what a bell curve looks like, but for whatever reason, I can't think of anything that would have that shape. Everything I am thinking of would have a skewed distribution where one tail was longer than the other.
Another related question - would it ever be possible for a curve to have two high spots compared to the curve going up and coming back down in a normal bell curve?
It seems counter intuitive that a positively skewed distribution would have a tail going to the right. I would have guessed that the positive and negative was determined by where the highest point of the curve was.
Post your comments