At AllTheScience, we're committed to delivering accurate, trustworthy information. Our expert-authored content is rigorously fact-checked and sourced from credible authorities. Discover how we uphold the highest standards in providing you with reliable knowledge.
What is the Difference Between Volume and Surface Area?
Volume and surface area are two related concepts in the study of mathematics. They’re both important to understand, but equally important is understanding how they differ and what they mean. This is especially the case when it comes to computing the volume and surface areas of a prism or a cylinder.
If you think of wrapping a present in a box, you can get a good sense of how volume and surface area differ. First, you have to consider the size of the box, when you consider the size of the present. How much interior space does your box need to have so a present will fit? The measurement of the box’s capacity, how much it will hold, is its volume. Next you have to wrap the present. The amount of wrapping paper, which will cover the exterior of the box, is a very different calculation than the capacity of the box. You’ll need a separate measurement or some good guessing, to figure out the sum of the sides of all the surfaces or the surface area.
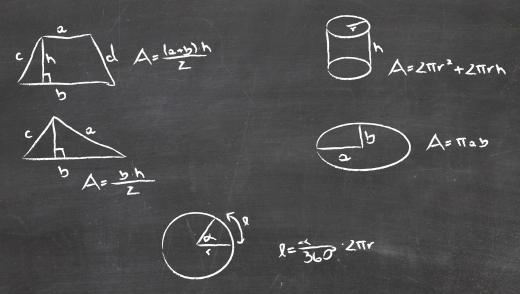
Volume of a square or rectangular box is pretty easy to compute. Simply multiply height times length times width to get the measurement. With a square it’s even easier, you merely cube one side’s length, since they all measure the same. If the side length is a, the formula is a x a x a or a3. When you are comparing volume and surface area, you’ll note a very different formula. You need to get the area of each face, and then add the areas of all faces together. With a square prism or cube, you’d essentially compute the area a x a or a2, multiplied by 6 (6a2). When you’re working with a rectangular prism, you’ll have to the area the of 3 pairs of equal sides, which needed to be added together to determine surface area.
Work on volume and surface area are differ a little when you are trying to calculate the area of a cylinder. The formula for a volume of a cylinder is the area of one circular face multiplied times the height of the cylinder. It reads: πr2 x h, or pi times the radius squared times height. Getting the surface area of the cylinder is a little trickier since the circular portion is essentially one continuous face. Computing surface area of a cylinder means computing the lateral area of this face.
Lateral area formula is the following πr2r or πd (pi times the radius doubled or pi times the diameter), multiplied to the height, πr2r x h. This is essentially the circumference of one circle times the height of the cylinder. To compute the entire formula you also need to add in the top and bottom circular faces’ areas. Since in a cylinder these are equal, the formula is 2 πr2. This calculation is then added to the lateral area to compute the whole surface area in the following expression:
πr2r x h + 2πr2 = lateral area.
You can also view difference between volume and cylinder as a difference between what is inside and can be contained and the exterior of a three-dimensional object. These are valuable differences to understand in many applications, such as construction, engineering, or even present wrapping. When children complain that math is useless outside of math class, you might point out to them that knowing the difference between volume and surface area meant they got a very nicely wrapped gift for their birthday.
AS FEATURED ON:
AS FEATURED ON:











Discussion Comments
For nanomaterials, if has a small surface area, will has a large pore volume; if has a big surface area, will has a small pore volume. Can use V-Sorb 2800P static volumetric principle to test it.
The volume of a cylinder=pi r square h, so half a cylinder's will be pi r 2 h/2.
@NathanG - In that case the volume is half. My understanding is that to come at the final number you would take half of the area of the cylinder’s base and multiply it by the height.
I understand cylinder volume but what about if I have half a cylinder? How do I calculate that? I know it sounds weird, but this is not an uncommon scenario in engineering applications.
One of the most practical applications for volume of sphere calculations is in astronomy. You use information about a planet's volume to calculate its density.
Density is basically mass divided by volume. Once you have that information, you can make comparisons between planets. Some planets will be less dense than others, for example, because they are made primarily of gas, while other planets are solids (like Earth). Regardless, you need to know volume to make the final calculation.
Post your comments