A sine wave, or sinusoid, is a mathematical construct (specifically a function) used to model and predict a variety of cyclic phenomena, including the rise and fall of tides, the oscillation of a spring, the incident light hitting the ground from the Sun over the course of a day, the intensity of a sound wave, and millions of other examples. The sine wave is usually the first function that students learn when studying pre-calculus (trigonometry). The most basic way of writing a sine wave function is f(x) = sinx, where "sin" means "sine," and x is the variable being operated on.

Practically everything in reality oscillates. All electromagnetic energy, including visible light, microwaves, radio waves, and x-rays, can be represented by a sine wave. At the lowest level, even matter oscillates like a wave, but for macroscopic objects, these oscillations are so minimal are to be impossible to measure. Sound waves can be represented as sine waves, and the up-and-down waves on an oscilloscope may be the most widely known representation of a sine wave. The study of sine waves and related functions is the most basic kind of higher (post-algebra) mathematics.

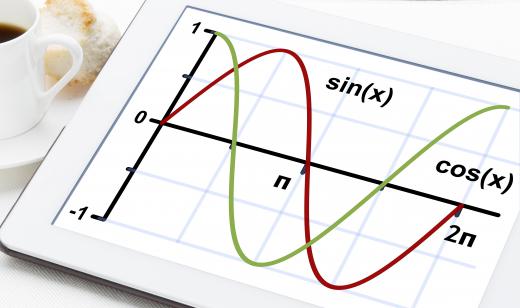
Besides appearing in sound waves, light waves, and ocean waves, the sine wave is also very important in electronics, as the intensity of an alternating current can be modeled by a sine wave. The current of a direct current full-wave rectification system, used to convert AC into DC, can be modeled using an absolute value sine wave, where the wave is similar to a normal sine wave because the value always stays above the x-axis, with twice as many peaks as a normal sine wave function. Along with the sine wave is its cousin, the cosine wave, which is exactly the same except displaced to the right by half a cycle.

In 1822, French mathematician Joseph Fourier discovered that any wave could be modeled as a combination of different types of sine waves. This applies even to unusual waves like square waves and highly irregular waves like human speech. The discipline of reducing a complex wave to a combination of sine waves is called Fourier analysis, and is fundamental to many of the sciences, especially those involving sound and signals. Fourier analysis is central to signal processing and the analysis of time series, where seemingly random sets of data points are studied to elucidate a statistical trend. Fourier analysis is also used in probability theory, where it is used to prove the central limit theorem, which helps to explain why bell curves, or normal distributions, are ubiquitous in nature.