At AllTheScience, we're committed to delivering accurate, trustworthy information. Our expert-authored content is rigorously fact-checked and sourced from credible authorities. Discover how we uphold the highest standards in providing you with reliable knowledge.
What is a Bell Curve?
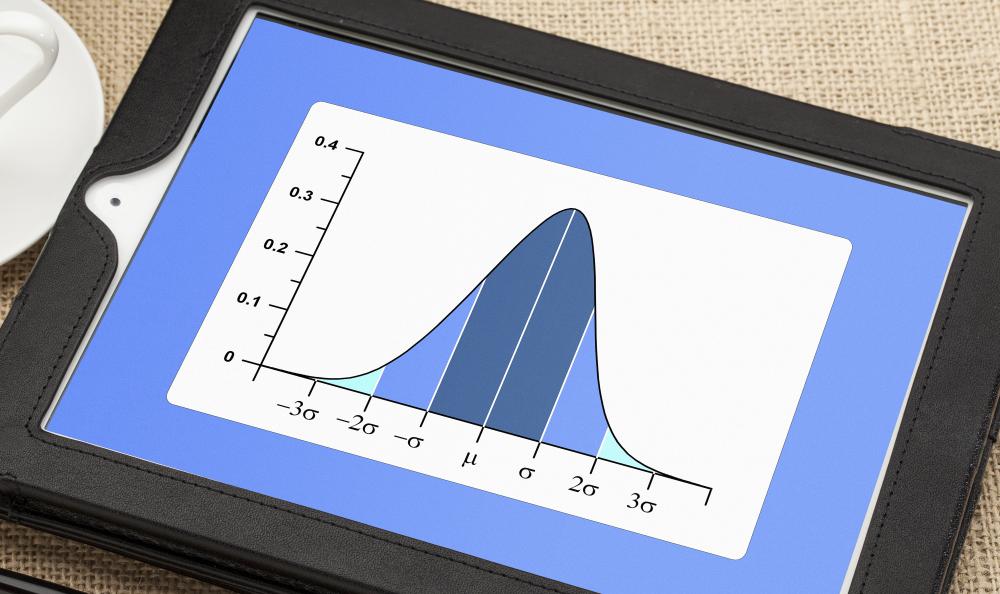
A bell curve is a graph which depicts a normal distribution of variables, in which most values cluster around a mean, while outliers can be found above and below the mean. For example, human height often follows a bell curve, with outliers who are unusually short and tall and the bulk of people being concentrated around a mean height, such as 70 inches (178 centimeters) for American men. When data which follows a normal distribution pattern is graphed, the graph often resembles a bell in cross section, explaining the term “bell curve.”
Normal or Gaussian distributions can be found in a wide variety of contexts, from graphs of the performance of financial markets to test scores. When variables are graphed and a bell curve appears, this is often taken to mean that the variables were within normal expectations, and that they are behaving in a predictable manner. If the graph is skewed or irregular, it can indicate that there is a problem.
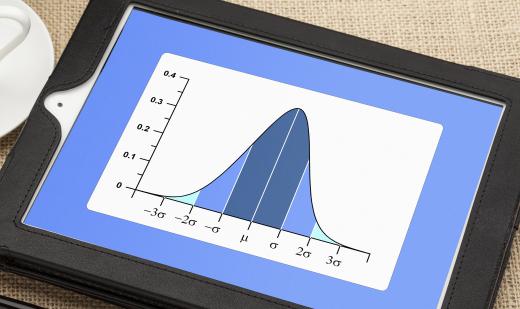
Ideally, a bell curve is symmetrical. In scoring, for example, a test should be written in such a way that a small number of students fail with an F, and an equally small number get a perfect score with an A. A slightly larger number of students should get Ds and Bs, and the largest number should get Cs. If the bell curve is skewed and the peak of the curve is in the Ds, it suggests that the test was too hard, while a test with a peak in the Bs is too easy.
Using a bell curve, it is also possible to arrive at the standard deviation for the data. The standard deviation shows how tightly packed the variables are around the mean. Standard deviations reflect the diversity of the variables being plotted, and they can be used to gather information about the validity of the data. A large standard deviation indicates that the variables are not tightly clustered, and that there may be a problem with the data, while small standard deviations suggest that the data may be more valid.
For example, when polls are conducted, the polling company releases standard deviations. If the standard deviation is small, it means that were the poll to be repeated, the data would be very close to that of the original poll, suggesting that the polling company used valid methods and that the information is accurate. If the standard deviation is large, however, it would indicate that repeat polls might not return the same results, making the data less useful.
AS FEATURED ON:
AS FEATURED ON:










Discussion Comments
I am often distressed to find myself at or near the bulk pinnacle of a bell curve, with only an average percentile in score. Even when I am near the top of the class, I want to find out who beat me and was closer to the top percentile.
The bell curve grading formula is often misleading when it is applied to IQ or a specific area. It is often very difficult to measure someone's intelligence based on a test, but easy to measure their preparedness. Stephen Hawking himself has said that he thinks IQ tests are stupid.
Simple and with good examples.
Post your comments